Multi Period Stationary Overlapping Generations Model

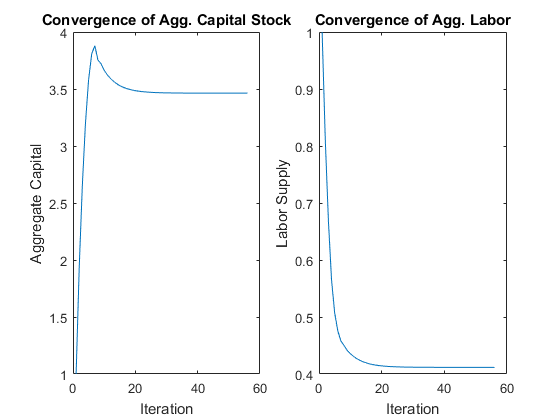
Assume an economy in which same number agents are born every period and live exactly 60 periods. In every period, agents make consumption/saving and labor supply decisions that maximize their utility. The solution is found using value function iterations over discretized grids.

Matlab function [download]

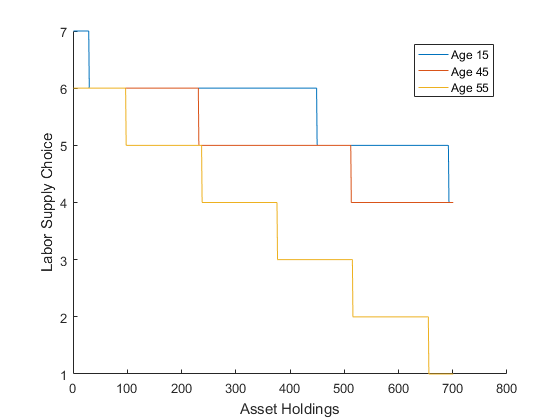
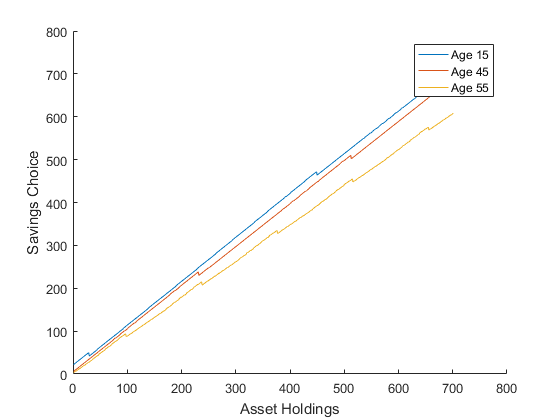
clearvars
global A alpha delta eta gamma
%Production parameters
A=1; alpha=0.5; delta=0.1;
%Agent and utility parameters
AGE=60; beta=0.95; eta=2; gamma=0.5;
%Discretized grids
kgrid=[0:0.01:7]'; ngrid=[0:0.1:0.9]';
smooth=0.8; eps1=0.00001; eps2=0.00001;
%Initialization
k1max=zeros(length(kgrid),AGE);
nmax=zeros(length(kgrid),AGE);
V=zeros(length(kgrid),length(ngrid));
dif=1; loop=1;
%Initial Guesses
K(loop)=1; N(loop)=1;

while dif>eps1
    %Value function iterations
    [~,w,r]=ProductionFunction(K(loop),N(loop));
    V1=zeros(length(kgrid),1);
    for age=AGE:-1:1
        for k=1:length(kgrid)
            for n=1:length(ngrid)
                c= kgrid(k)*(1+r) + ngrid(n)*w - kgrid ;
                c= (c).*(c>0);
                V(:,n)=UtilityFunction(c+eps2,ngrid(n))+beta*V1;
            end
            [k1max(k,age),nmax(k,age)]=find(V==max(max(V)));
            Vmax(k,1)=V(k1max(k,age),nmax(k,age));
        end
        V1=Vmax;
    end
    k0=1;
    for i=1:AGE
        k_opt(i)=k0;
        n_opt(i)=nmax(k0,i);
        k1_opt(i)=k1max(k0,i);
        k0=k1_opt(i);
    end
    K1(loop)=sum(kgrid(k_opt))/AGE;
    N1(loop)=sum(ngrid(n_opt))/AGE;
    dif(loop)=abs(K1(loop)-K(loop));
    loop=loop+1;
    K(loop)=K(loop-1)*smooth+K1(loop-1)*(1-smooth);
    N(loop)=N(loop-1)*smooth+N1(loop-1)*(1-smooth);
end

figure; hold on; plot(nmax(:,15)); plot(nmax(:,45)); plot(nmax(:,55));
xlabel('Asset Holdings');ylabel('Labor Supply Choice');
legend('Age 15', 'Age 45', 'Age 55');

figure; hold on; plot(k1max(:,15)); plot(k1max(:,45)); plot(k1max(:,55));
xlabel('Asset Holdings');ylabel('Savings Choice');
legend('Age 15', 'Age 45', 'Age 55');

function[u]=UtilityFunction(c,n)
global eta gamma
u=(((c.^gamma).*(1-n)^(1-gamma)).^(1-eta)-1)./(1-eta);
end

function[Y,w,r]=ProductionFunction(K,N)
global A alpha delta
Y=A*(K^alpha)*(N^(1-alpha));
w=(1-alpha)*A*(K^alpha)*(N^(-alpha));
r=alpha*A*(K^(alpha-1))*(N^(1-alpha))-delta;
end